Una ecuación de primer grado o ecuación lineal es una igualdad que involucra una o más variables a la primera potencia y no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a la primera potencia.

Para entender mejor al tema, muestro el siguiente glosario glosario:

ECUACION:es una igualdad matemática entre dos expresiones, denominadas miembros y separadas por el signo igual, en las que aparecen elementos conocidos o datos, desconocidos o incógnitas.

IGUALDAD MATEMATICA:Dos objetos matemáticos son considerados iguales si los objetos poseen el mismo valor, esta se representa con un signo =

 INCOGNITA: es un elemento desconocido de una expresión matemática.

VARIABLE:es un símbolo que puede ser reemplazado o que toma un valor numérico en una ecuación o expresión matemática en general.

EJEMPLO DE LA RESOLUCIÓN DE UNA ECUACIÓN DE PRIMER GRADO:

Ecuación 

Solución:Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.Como 8 está restando en la derecha, pasa sumando al lado izquierdo:

Como x está restando en la izquierda, pasa restando a la derecha:

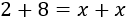
Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos 2+82+8 y, en la derecha, x+xx+x:

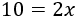
Para ver con claridad el paso siguiente, escribimos 2x2x como un producto:

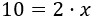
Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a xx) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:

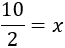
Simplificando la fracción,

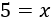
Por tanto, la solución de la ecuación es x=5x=5. Para comprobar la solución, sustituimos xx por 5 en la ecuación:

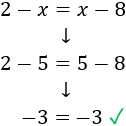
Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.

Ahora podemos comenzar mencionando que estas ecuaciones reciben también el nombre de ecuaciones lineales puesto a que al representar su trazo en un sistema de coordenadas se obtiene una linea recta, como en el siguiente ejemplo:

Un ejemplo resumido de como graficar es la siguiente: trace la gráfica de la ecuación 

 Solución:despejamos a y, y que da que y: 2 x-5

Damos un valor cualquiera para x, por ejemplo 2 ( x: 2).Ahora el valor de y, dependerá del valor correspondiente al realizar la operación correspondiente:

y:2 x-5

y:2(2)-5

y:4-5

y:-1

esto es cuando, equis vale dos, ye vale -1.Entonces las coordenadas quedan (2,-1)

Ahora buscamos el valor de otro numero, como el 3. Y queda que:

y:2 x-5

y:2(3)-5

 
y:6-5

 
y:1

Y obtenemos la segunda coordenada que es (3,1).Ahora graficamos estos dos pares ordenados que son (2,-1) y (3,1), puesto a que con solo dos coordenadas podemos lograr obtener nuestra grafica y obtenemos la siguiente: